Mark Humphries’ lab at the University of Nottingham School of Psychology.
We are a neural data lab.
We interrogate how the joint activity of many neurons encodes the past, present, and future in order to guide behaviour. We develop analysis techniques for neural data, and use them to understand what the joint activity is encoding in recordings of hundreds or thousands of neurons, across different tasks, brain circuits, species, and phyla. And we develop theoretical and computational models for how this joint activity arises from neural circuits.
Supported by the Medical Research Council, the BBSRC, and Innovate UK.
Highlights
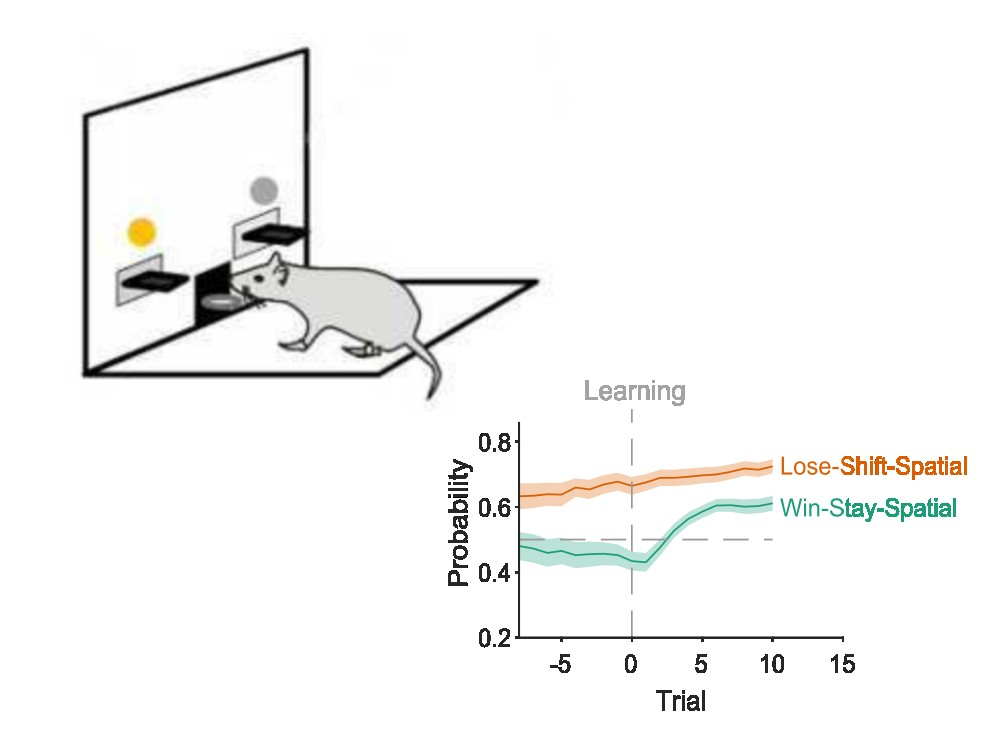
Strategy Tracker
Investigating how, when, and what subjects learn during decision-making tasks requires tracking their choice strategies on a trial-by-trial basis. In our new paper, we present a simple but effective probabilistic approach to tracking choice strategies at trial resolution. We show it identifies both successful learning and the exploratory strategies used in decision tasks performed by humans, non-human primates, rats, and synthetic agents.
Strategy Tracker is available in Python and MATLAB.
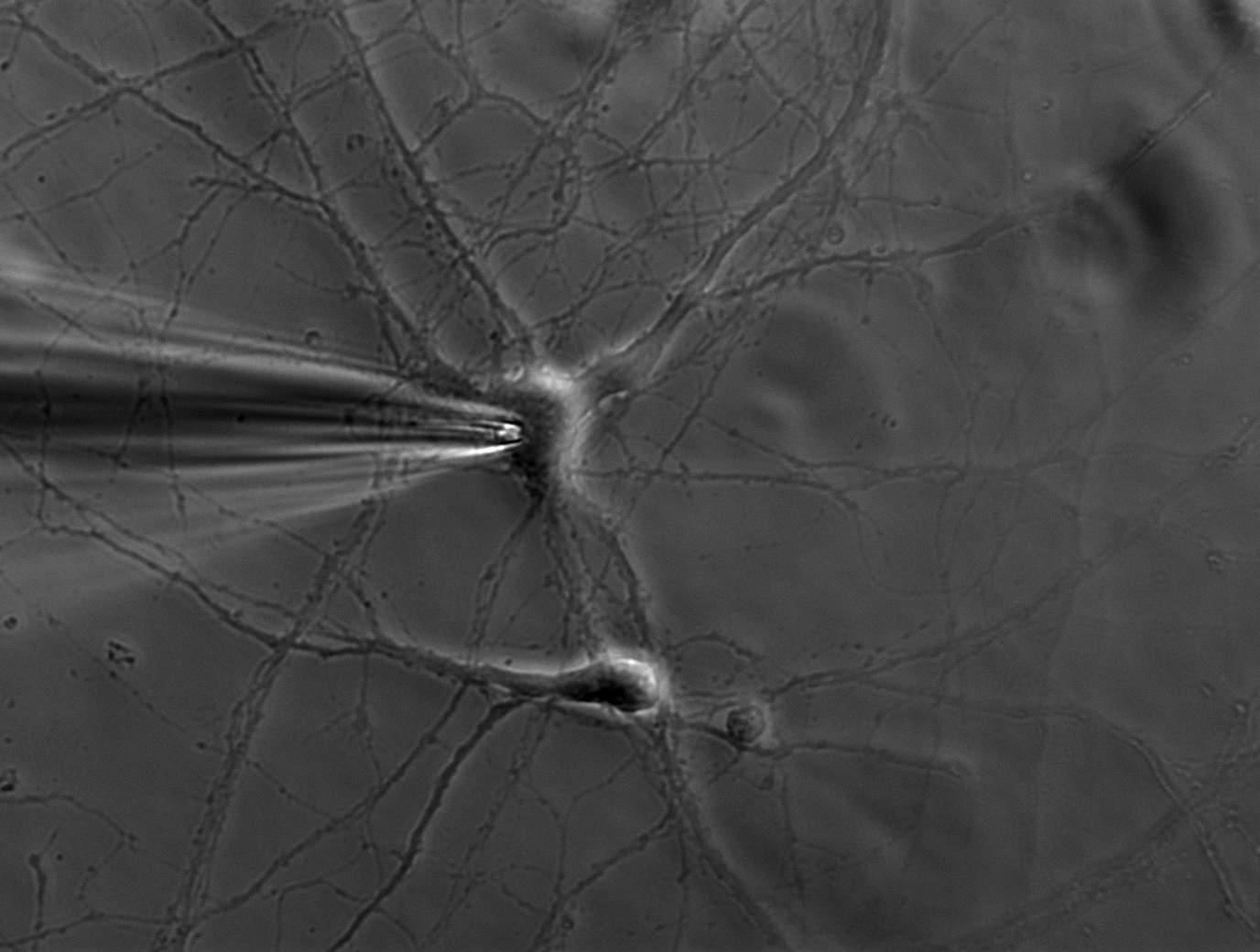
Computing the probability of connection between two neurons
A new Bayesian approach to computing the probability of connection between classes of neuron from paired recordings. Our algorithm outputs the probability of connection, the strength of evidence for it, and how it depends on distance between neurons. We use this approach to synthesise the most complete map of the striatal microcircuit currently available.
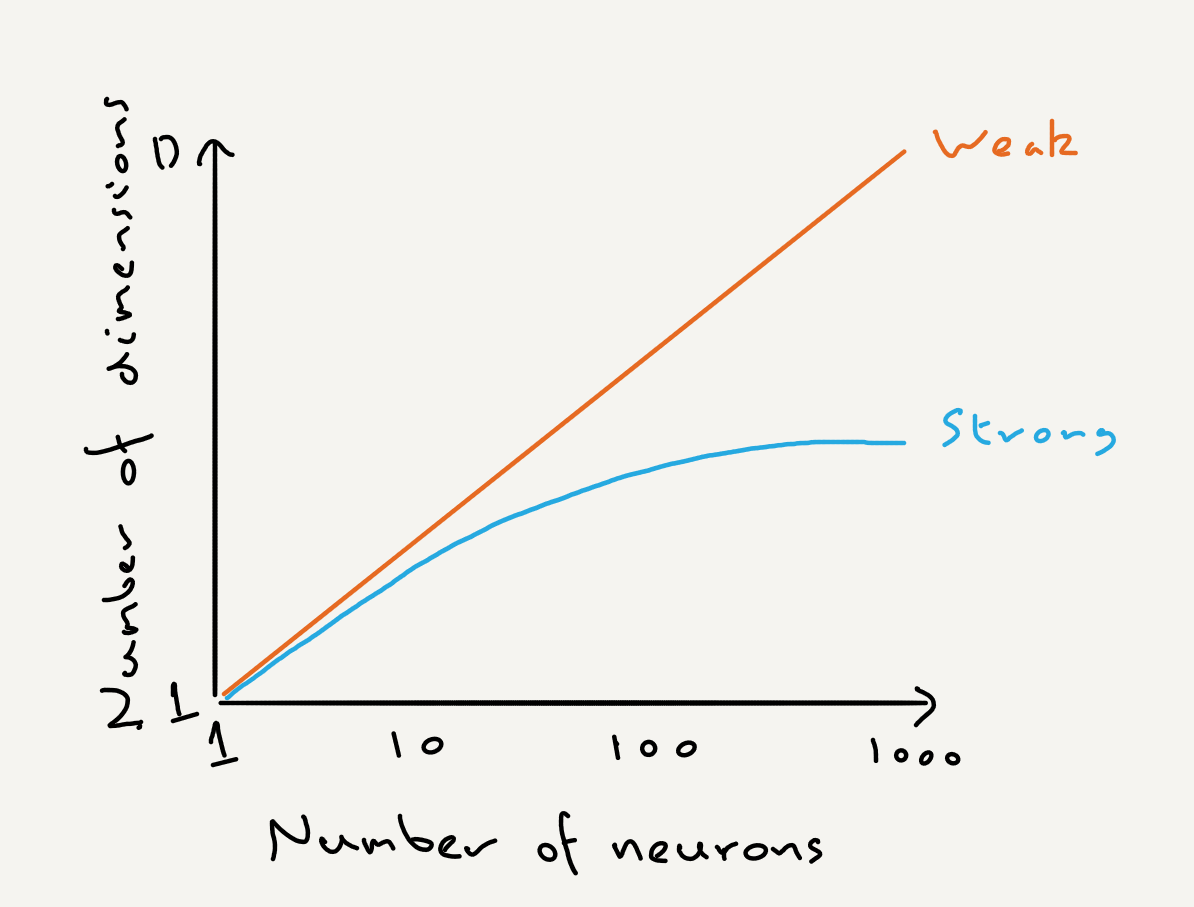
Strong and weak principles of neural dimension reduction
When we apply dimension reduction to neural activity how should we interpret its output? Mark’s paper argues for strong and weak principles of neural dimension reduction: The weak principle is that dimension reduction is a convenient tool for making sense of complex neural data; the strong principle is that dimension reduction shows us how neural circuits actually operate and compute.
The strong and weak principles make different predictions about how we might expect the dimensionality of neural activity to scale with the number of neurons; these predictions were recently tested by Manley et al (2024) Neuron.
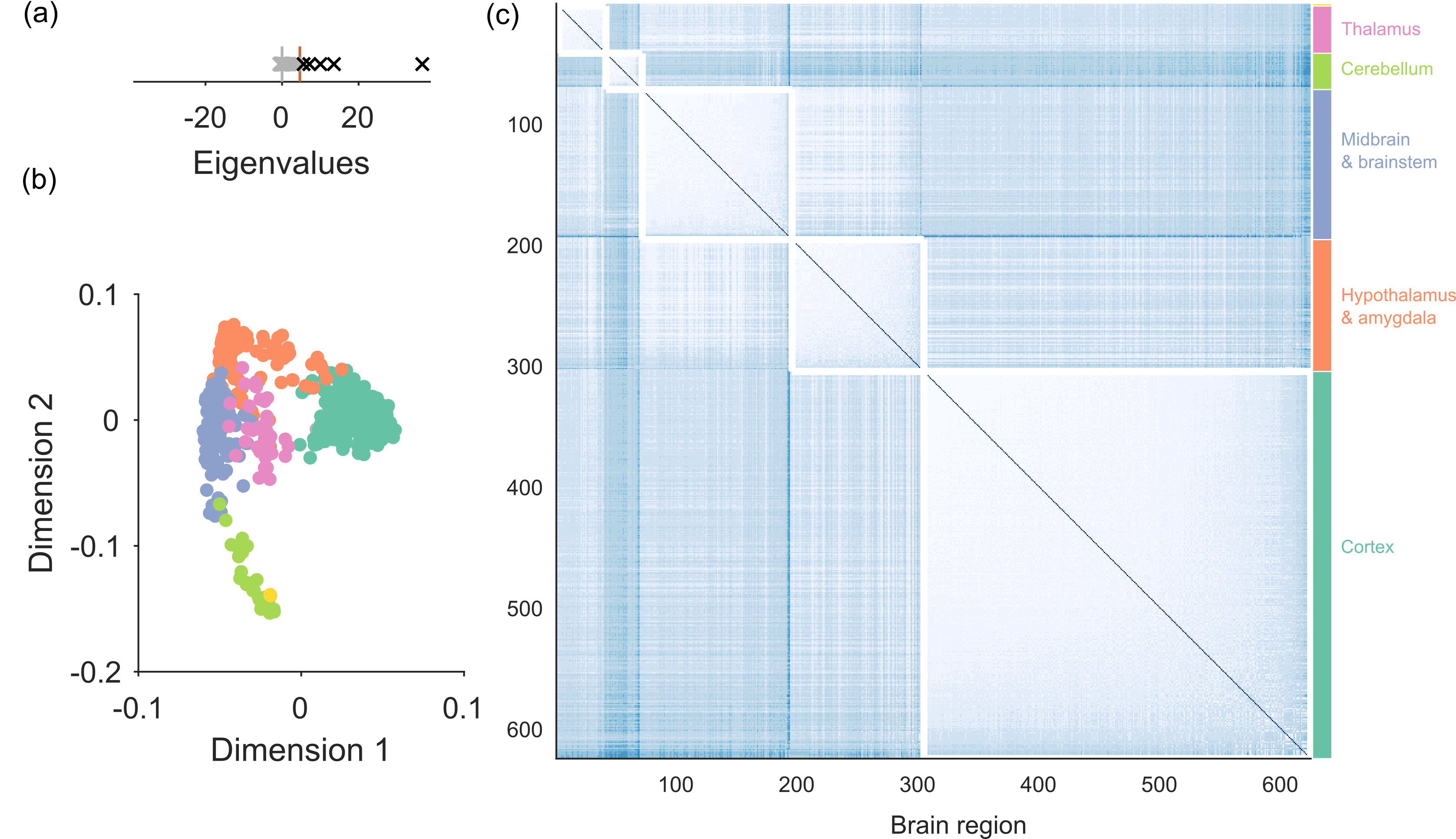
Finding the dimensions of networks
Discovering low-dimensional structure in networks requires a suitable null model that defines the absence of meaningful structure. Here we introduce a spectral approach for detecting a network’s low-dimensional structure, and the nodes that participate in it, using any null model. A powerful feature of our approach is that it automatically estimates the number of dimensions in the data network that depart from the null model.
This paper was the result of whole-lab hackathons by Humphries, Caballero, Evans, Maggi & Singh.